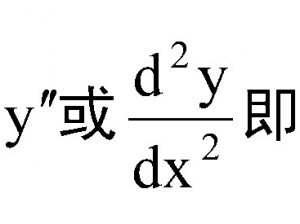- 01导数和微分的简介
- 02微分的简介和定义
- 03导数与微分的基本性质一
- 04导数与微分的基本性质二
- 05Rolle罗尔定理
- 06微分中值定理
- 07数学微积分_柯西中值定理
- 08微分学的链式法则连锁律的说明
- 09函数可导必定连续的证明
- 10幂函数的导数公式(次幂为自然数)
- 11幂函数的导数公式(次幂为实数)
- 12多项式微分公式的几何记忆法
- 13三角函数导数与微分公式
- 14三角函数导数公式的几何意义
- 15反函数的介绍和微分法则
- 16反三角函数的微分和求导法则
- 17反三角函数arcsec的微分公式和图形说明
- 18对数函数的微分公式
- 19含绝对值的对数函数微分公式
- 20指数函数的微分公式(反函数法)
- 21幂指函数的导数公式
- 22双曲函数的导数与微分公式推导
- 23反双曲函数的导数与微分公式推导
- 24高阶导数简介与常用公式
- 25可导和可微互为充要条件的证明
- 26求法線的方程式
- 27牛顿法求函数的根
- 28洛必达法则l'H?pital's rule一
- 29洛必达法则l'H?pital's rule二
- 30洛必达法则比较无穷大无穷小
- 31隐函数微分法简介
- 32隐函数微分法证明幂函数的导数公式(次幂为分数)
- 33隐函数微分法求高阶导数公式的例子
- 34参数方程式的导数公式
- 35摆线方程式的推导以及导数与微分技巧
- 36微分法求函数的近似值
- 37导数与相关变化率的观念说明
什么叫做导数,什么叫做微分?导数和微分的关系,一个是手心,一个是手背,微粉的极限就是导数。可以简单地理解,导数可以看做是切线的斜率。不管是导数还是微分,都是建立在极限的基础上的,大家在学习的过程中一定要对极限有一个清晰地认识。