- 第1章 初等积分法 常微分方程的发展简史
- 第1章 初等积分法 常微分方程的学科特征
- 第1章 初等积分法 1.1微分方程
- 第1章 初等积分法 1.2通解与特解
- 第1章 初等积分法 1.3初值问题
- 第1章 初等积分法 1.4解的几何意义
- 第1章 初等积分法 2.1变量可分离方程的解法
- 第1章 初等积分法 2.2分离变量法的解题原理
- 第1章 初等积分法 2.3齐次方程的解法
- 第1章 初等积分法 2.4应用举例
- 第1章 初等积分法 3.1一阶线性微分方程
- 第1章 初等积分法 3.2伯努利方程
- 第1章 初等积分法 3.3证明题与应用题选讲
- 第1章 初等积分法 4.1全微分方程及其解法
- 第1章 初等积分法 4.2积分因子
- 第1章 初等积分法 4.3应用举例
- 第1章 初等积分法 5.1一阶隐式方程可积类型1
- 第1章 初等积分法 5.2一阶隐式方程可积类型2
- 第1章 初等积分法 6.1第二种可降阶的高阶方程
- 第1章 初等积分法 6.1恰当导数方程
- 第1章 初等积分法 6.1三种可降阶的高阶方程
- 第1章 初等积分法 6.2高阶方程应用举例
- 第1章 初等积分法 6.3初等积分法小结
- 第2章 基本定理 7.1解的存在性
- 第2章 基本定理 7.2解的唯一性
- 第2章 基本定理 7.3几点说明
- 第2章 基本定理 8.1延展解不可延展解的定义
- 第2章 基本定理 8.2不可延展解的存在性
- 第2章 基本定理 8.3不可延展解的性状
- 第2章 基本定理 9.1奇解
- 第2章 基本定理 9.2包络线及奇解的求法
- 第2章 基本定理 9.3习题选讲
- 第2章 基本定理 f(x,y)与解存在区间的关系
- 第2章 基本定理 不可延展解的存在区间
- 第2章 基本定理 解整体存在的条件
- 第3章 一阶线性微分方程组 10.1一阶微分方程组
- 第3章 一阶线性微分方程组 10.2一阶线性微分方程组
- 第3章 一阶线性微分方程组 10.3一阶线性齐次微分方程组的通解结构
- 第3章 一阶线性微分方程组 11.1一阶线性非齐次微分方程组的通解结构
- 第3章 一阶线性微分方程组 11.2拉格朗日常数变易法
- 第3章 一阶线性微分方程组 11.2习题选讲
- 第3章 一阶线性微分方程组 12.1单特征根情形
- 第3章 一阶线性微分方程组 12.2复值解实值化
- 第3章 一阶线性微分方程组 12.3重特征根情形简介
- 第4章 n阶线性微分方程 (1)有关解的存在唯一性的证明题
- 第4章 n阶线性微分方程 (2)与朗斯基行列式有关的习题
- 第4章 n阶线性微分方程 (3)关于解的渐进性质的证明题
- 第4章 n阶线性微分方程 13.1线性微分方程的一般概念
- 第4章 n阶线性微分方程 13.2 n阶线性齐次微分方程的一般理论
- 第4章 n阶线性微分方程 13.3 n阶线性非齐次微分方程的一般理论
- 第4章 n阶线性微分方程 13.4例题选讲
- 第4章 n阶线性微分方程 14.1特征根为单根情形
- 第4章 n阶线性微分方程 14.2特征根为重根情形
- 第4章 n阶线性微分方程 15.1第一类型非齐次项特解的待定系数解法
- 第4章 n阶线性微分方程 15.2第二类型非齐次项特解的待定系数解法
- 第4章 n阶线性微分方程 15.3二阶常系数线性方程与振动现象
- 第4章 n阶线性微分方程 n阶常系数线性齐次方程
- 第4章 n阶线性微分方程 重复根的复值解实值化
- 第5章 定性和稳定性理论简介 16.1稳定性的概念
- 第5章 定性和稳定性理论简介 16.2李雅普诺夫第二方法
- 第5章 定性和稳定性理论简介 17.1相平面,相轨线与相图
- 第5章 定性和稳定性理论简介 17.2初等奇点附近的轨线分布
- 第5章 定性和稳定性理论简介 17.3常点与奇点
- 第5章 定性和稳定性理论简介 17.4平面自治系统的三个基本性质
- 第5章 定性和稳定性理论简介 18.1极限环
- 第5章 定性和稳定性理论简介 18.2全局结构
- 第5章 定性和稳定性理论简介 18.3生物数学中的一个例子
- 常微分方程 总复习
在数学分析中,常微分方程(ordinary differential equation)是未知函数只含有一个自变量的微分方程。
很多科学问题都可以表示为常微分方程,例如根据牛顿第二运动定律,物体在力的作用下的位移 s 和时间 t 的关系就可以表示为如下常微分方程:
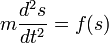 ;
; 这类问题就是要去寻求满足某些条件的一个或者几个未知函数。也就是说,凡是这类问题都不是简单地去求一个或者几个固定不变的数值,而是要求一个或者几个未知的函数。解这类问题的基本思想和初等数学解方程的基本思想很相似,也是要把研究的问题中已知函数和未知函数之间的关系找出来,从列出的包含未知函数的一个或几个方程中去求得未知函数的表达式。